这是一道可以用动态规划解的问题

题目

给定一个数组，找出其中等差数列的个数。等差数列的定义：3 各元素以上，每个元素之间差相等。

比如：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的就不是：

1, 1, 2, 5, 7

例子：

A = [1, 2, 3, 4]

return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.

解法

观察发现，当我们遍历数组的时候，如果能和前一个元素构成等差数列，那么在这个位置可以构成的等差数列的个数就是上一个位置加一，所以的到递推公式：

dp[i] = dp[i-1] + 1

借用官方答案里的图片：

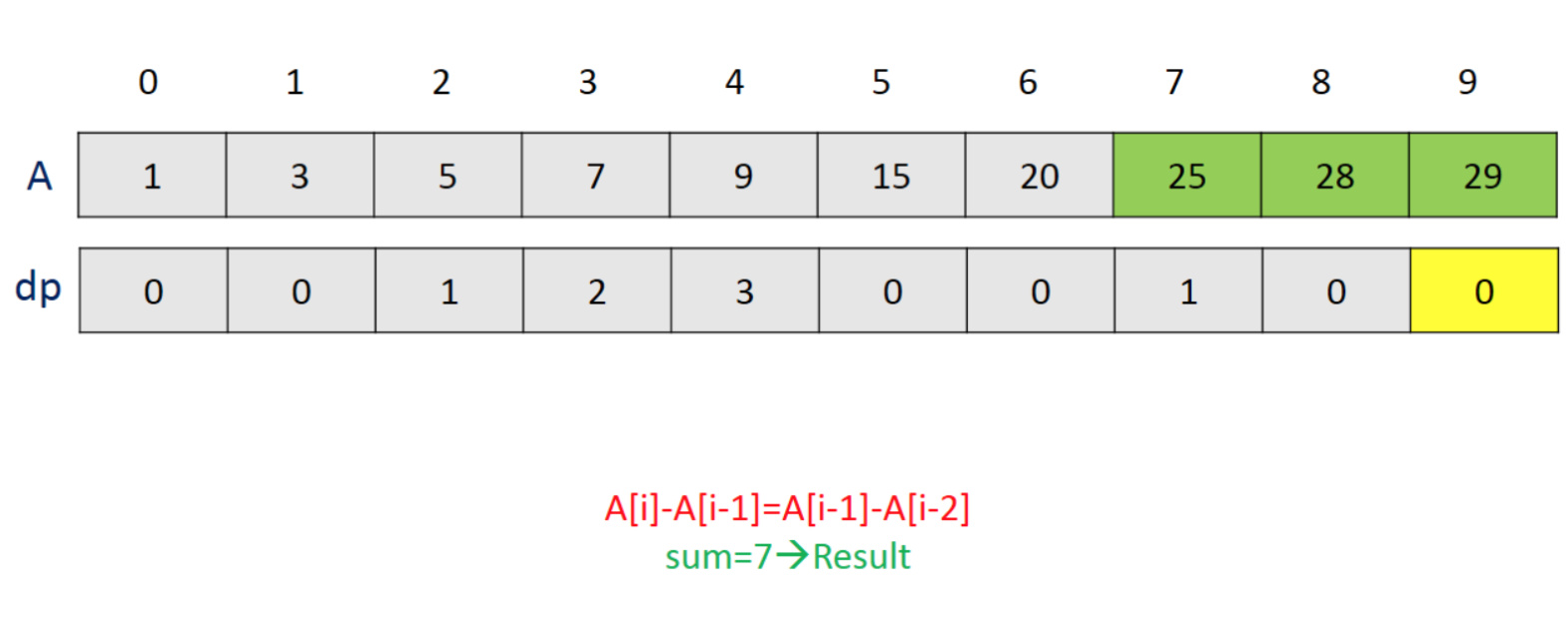
所以我们就得到了答案：

class Solution:
    def numberOfArithmeticSlices(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        dp = [0] * len(A)
        for i in range(2, len(A)):
            if A[i] - A[i-1] == A[i-1] - A[i-2]:
                dp[i] = dp[i-1] + 1

        return sum(dp)